前言
首先要说明的是: 这本书的定义是一本算法入门书,更多的是以简单地描述和示例介绍常见的数据结构和算法以及其应用场景,所以如果你在算法上有了一定造诣或者想深入学习算法,这本书很可能不太适合你。
但如果你对算法感兴趣,但是不知从何学起或者感觉晦涩难懂,这本书绝对是一本很好的入门书,它以简单易懂的描述和示例,配以插画,向我们讲解了常见的算法及其应用场景。
本文是我基于自己的认知总结本书比较重点的部分,并不一定准确,更不一定适合所有人,所以如果你对本书的内容感兴趣,推荐阅读本书,本书总计180+页,而且配以大量示例和插画讲解,相信你很快就可以读完。
第一章:算法简介
算法是一组完成任务的指令。任何代码片段都可以视为算法。
二分查找
二分查找是一种用来在有序列表中快速查找指定元素的算法,每次判断待查找区间的中间元素和目标元素的关系,如果相同,则找到了目标元素,如果不同,则根据大小关系缩短了一半的查找区间。
相比于从头到尾扫描有序列表,一一对比的方式,二分查找无疑要快很多。
在有序队列中,每次对半查找,最多查找次数:logn次,如32长度 需要查找log32 = 5次。
大O表示法
大O表示法是一种特殊的表示法,指出了算法的运行时间或者需要的内存空间,也就是时间复杂度和空间复杂度。
简单查找:O(n)/线性时间:多个元素则需要执行多少次,二分查找O(logn)/对数时间:如第一点;大O表示法通常用来 表示一个算法最糟糕情况下的运算时间/执行次数(算法的速度并非指时间,而是操作次数的增速)
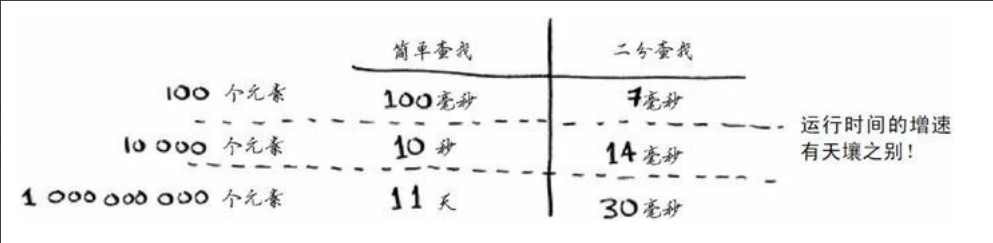
比如冒泡排序,
export default function bubbleSort(original:number[]) {
const len = original.length
for (let i = 0; i < len - 1; i++) {
for (let j = 1; j < len - i; j++) {
if (original[j - 1] > original[j]) {
[original[j - 1], original[j]] = [original[j], original[j - 1]]
}
}
}
}
需要两层循环,每次循环的长度为 n(虽然并不完全等于 n),那它的时间复杂度就是 O(n²)。同时因为需要创建常数量的额外变量(len,i,j),所以它的空间复杂度是 O(1)。
常见大O算法:

第二章:选择排序
内存的工作原理
当我们去逛商场或者超市又不想随身携带着背包或者手提袋时,就需要将它们存入寄存柜,寄存柜有很多柜子,每个柜子可以放一个东西,你有两个东西寄存,就需要两个柜子,也就是计算机内存的工作原理。计算机就像是很多柜子的集合,每个柜子都有地址。
内存比作一个柜子,柜子里有很多抽屉,这个抽屉就是内存单元,当需要寄存的时候,内存会找到空的抽屉,抽屉的地址就内存单元地址。
数组和链表
数组在在内存中必须是连续的,在内存中表现为连续相邻的内存单元。链表是不必要连续的,在内存中表现为随机,但是每个内存单元中有指向他下一节点的指针。如果使用数组,则需要定义它的长度,否则数组满了之后内存需要重新分配数组的地址(因为它的内存单元的下一个地址可能被占用),而使用链表则不会有这个问题。
数组优势:读取方便,因为知道每个元素的内存单元是连续的,内存地址很容易读取(随机读取、顺序读取),而访问链表中的某一个元素时 它的内存地址是不知道的,他的内存地址只有它的上一个元素有记录,所以得从第一个开始一次查找(顺序读取)。
链表优势:插入元素时只需要放入内存并将其地址存储在前一个元素之中。数组需要移动其他元素的地址。
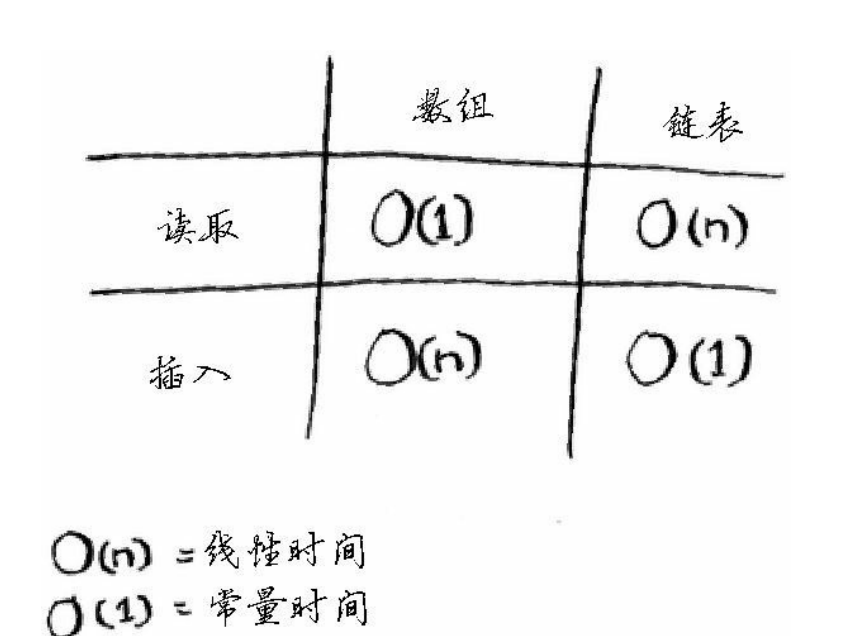
数组因为可以通过索引获取元素,所以其读取元素的时间复杂度为 O(1),但是因为其连续性,在中间插入或者删除元素涉及到其他元素的移动,所以插入和删除的时间复杂度为 O(n)。
链表因为只存储了链表的头节点,获取元素需要从头节点开始向后查找,所以读取元素的时间复杂度为 O(1),因为其删除和插入元素只需要改变前一个元素的next指针,所以其插入和删除的时间复杂度为 O(1)。
选择排序
选择排序就是每次找出待排序区间的最值,依次轮训查找满足条件的值放入新数组,时间复杂度:O(n*2)
第三章:递归
递归就是以相同的逻辑重复处理更深层的数据,直到满足退出条件或者处理完所有数据。
其中退出条件又称为基线条件,其他情况则属于递归条件,即需要继续递归处理剩余数据。
核心:循环调用自己,关键条件:基线条件和递归条件
基线条件:函数不再继续调用自己
递归条件:函数继续调用自己的条件
栈
栈:先进后出原则,如一堆盘子 只能操作顶部元素。
调用栈:计算机执行程序时会将所有需要执行的函数按实际顺序压入栈中,执行完毕后弹出栈的过程就是一个调用的栈,栈越高,消耗内存越大。实际应该尽量避免栈的堆积,因为递归函数是不断调用自身,所以就导致调用栈也来越大,因为每次函数调用都会占用内存,当调用栈很高,就会导致内存占用很大的问题。解决这个问题通常有两种方法:
- 将递归改写为循环
- 使用尾递归
第四章:快速排序
快速排序使用的是分而治之的策略。
分而治之
简单理解,分治就是将大规模的问题,拆解为小规模的问题,直到规模小到很容易处理,然后对小规模问题进行处理后,再将处理结果合并,得到大规模问题的处理结果。
第五章:散列表
散列表类似于JavaScript中的array、object和map,只不过作为上层语言,JavaScript帮我们做了很多工作,不需要我们自己实现散列函数,而散列函数,简单理解就是传入数据,会返回一个数字,而这个数字可以作为数组的索引下标,我们就可以根据得到的索引将数据存入索引位置。一个好的散列函数应该保证每次传入相同的数据,都返回相同的索引,并且计算的索引应该均匀分布。
散列表由散列函数+数组组成。数组存储实际查询值,散列函数是将输入映射到一个索引,它的特点是相同的输入映射到相同的索引,一个好的散列函数输入和输出的唯一对应的。通过散列函数输入得到索引,根据数组随机读取的特性,可以直接获取到数组存储的值。散列函数和数组就组成了散列表。散列表的读取速度很快,时间复杂度为O(1)。
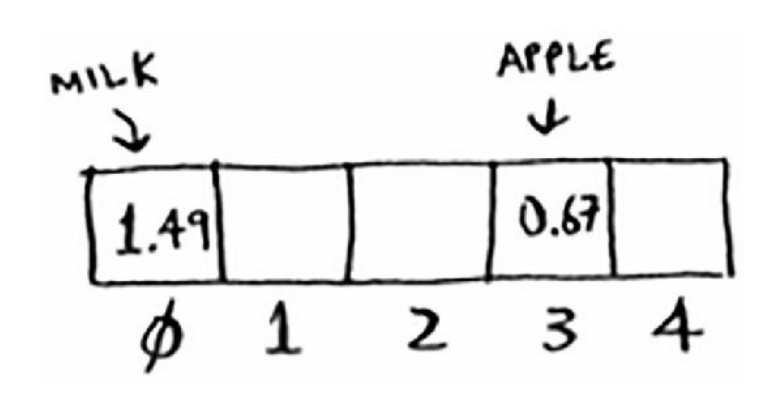
常见的散列表的应用有电话簿,域名到IP的映射表,用户到收货地址的映射表等等。
散列表常见应用:因为它读取速度快的特性可以用于缓存数据。
散列表的冲突:当两个键值对映射到同一个位置,原来的值会被覆盖掉。冲突的解决:在这个位置上建立一个链表,但是会导致访问速度变慢,如果散列函数所有的映射都是同一个位置,那么等同于链表顺序读取,就非常缓慢,所以散列函数应该尽量避免映射到同一个位置,应该均匀的映射,一个好的散列函数就尤为重要。
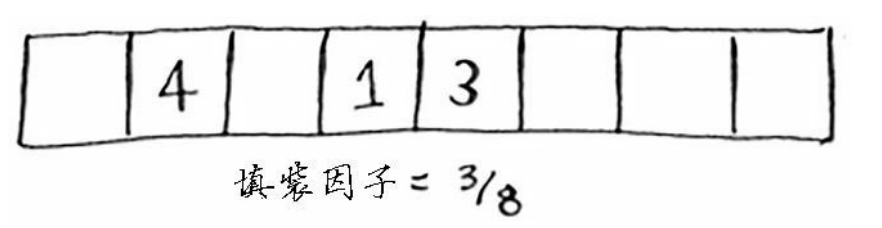
散列表的性能:较低的填充因子(度量散列表中的空余位置,空余位置越少说明填充度越高,每个元素分配越合理,填充因子越小,发生冲突的可能性越小,散列表的性能就越高)、良好的散列函数(能够让数组的值呈现均匀分布,如sha函数一样,应该固定输入对应固定输出,输出是唯一的)这样就不会造成散列表中链表的情况存在)
第六章:广度优先搜索
图
图由节点和边组成,一个节点可以和多个节点相连,相邻的两个节点称为邻居。
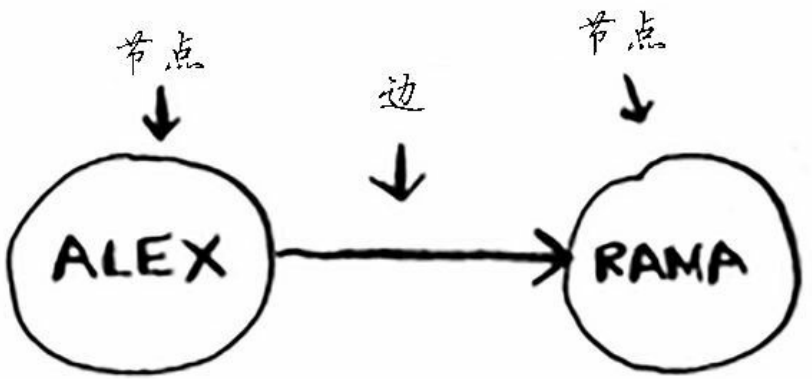
有向图:节点之间的指向有方向,关系为向的图
无向图:节点直接没有方向,互为邻居,下面两个图等价

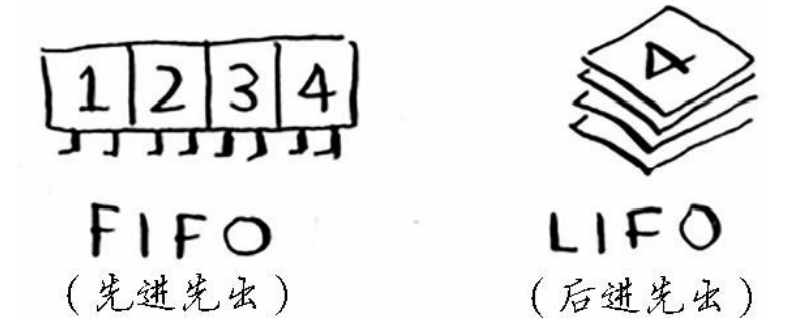
队列
队列只支持两种操作:出队入队。先进先出(栈是后进先出)
广度优先搜索
回答两类问题:1:是否存在某条路径?2、最短路径问题 时间复杂度:O(V+E) v为顶点数,e为边数。
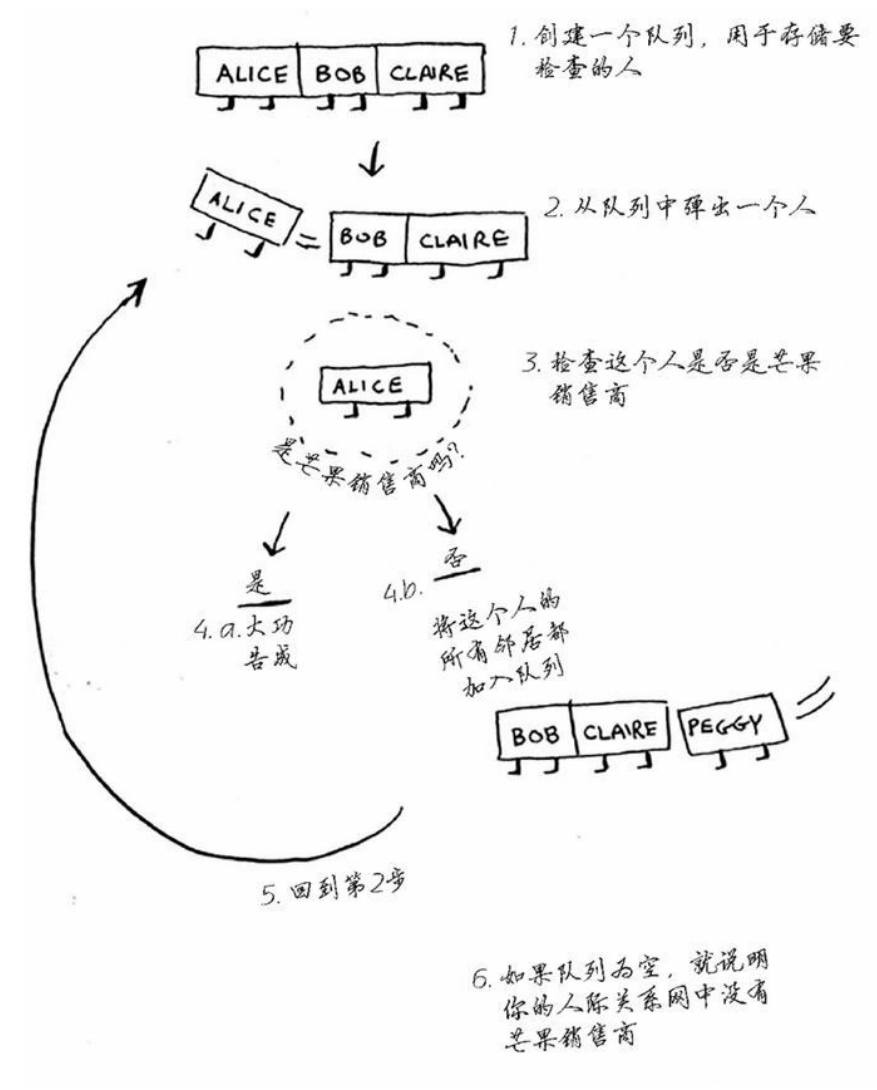
示例:在朋友中寻找关系最近的芒果经销商:
算法介绍:创建一个队列,将朋友加入这个队列,如果这个队列不为空,弹出元素,判断这个元素是否满足条件,不满足则将他朋友压入队列,同时检测完一个元素后需要将这个元素push到一个数组中标记这个元素已经检测过(否则会无限循环),因为它可能是其他节点的邻居。然后继续轮询查找直到找到满足条件的元素。
拓扑排序
如广度优先算法创建队列的逻辑,但是有点不同的是 如果两个节点有依赖关系,如A需要在B后面执行,则这个队列要有序。最后排出来的队列就是拓扑排序。
树
是一种特殊的图,它所有的边的方向是相同的 且兄弟节点间是没有指向的。(常见结构 不做过多解释)
第七章:狄克斯特拉算法
当一个图需要找到最短路径时,我们可以使用广度优先算法找到最短路径,但是如果给图的边加上权重(如时间),那么最短路径需要的时间不一定是最短时间。而狄克斯特拉算法则是实现了总权重最小的路径算法。如下图
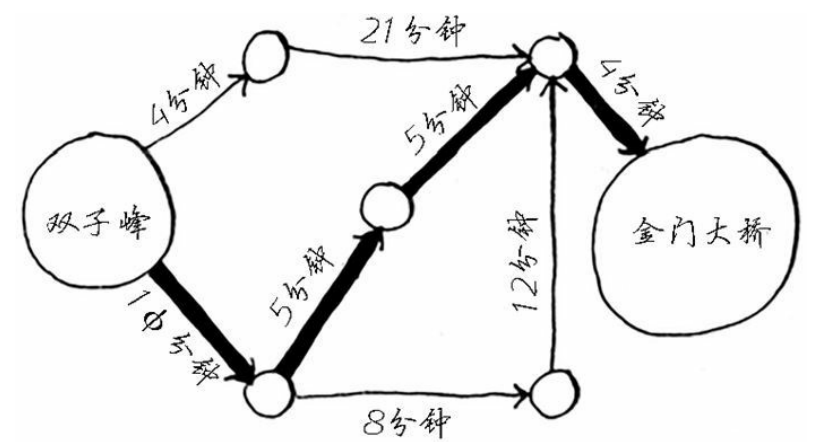
狄克斯算法的关键步骤:
-
1、找到最便宜的节点。
-
2、对于该节点的邻居,检查是否有前往它们的更短路径,如果有则更新他们的开销,
-
3、重复这个过程,对每一个节点进行这样判断更新开销(终点例外),
-
4、计算最终路径
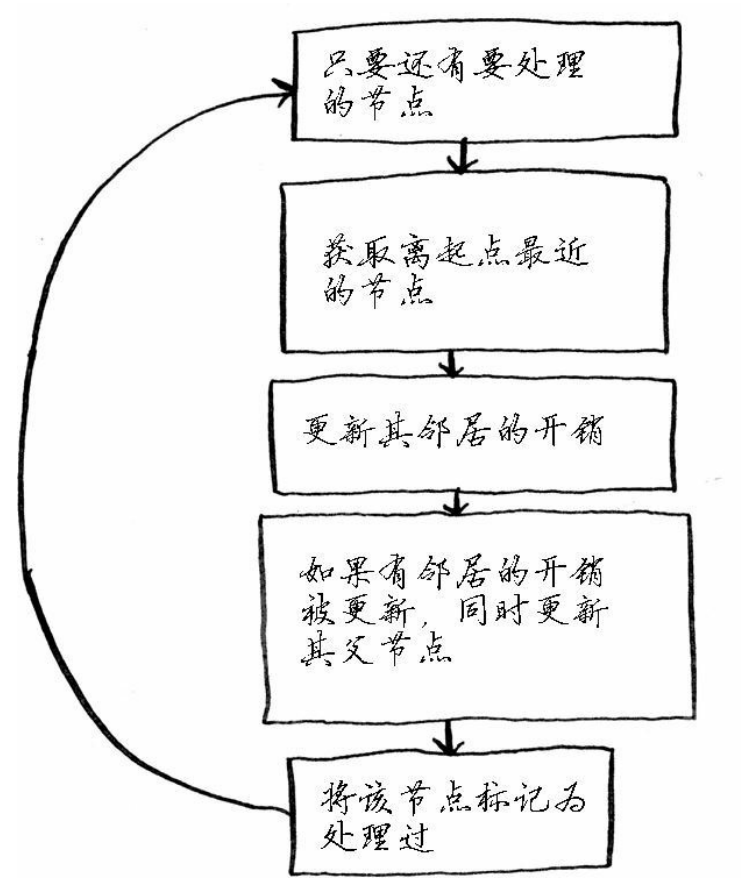
这个算法只适用于有向无环图且权重为正。


